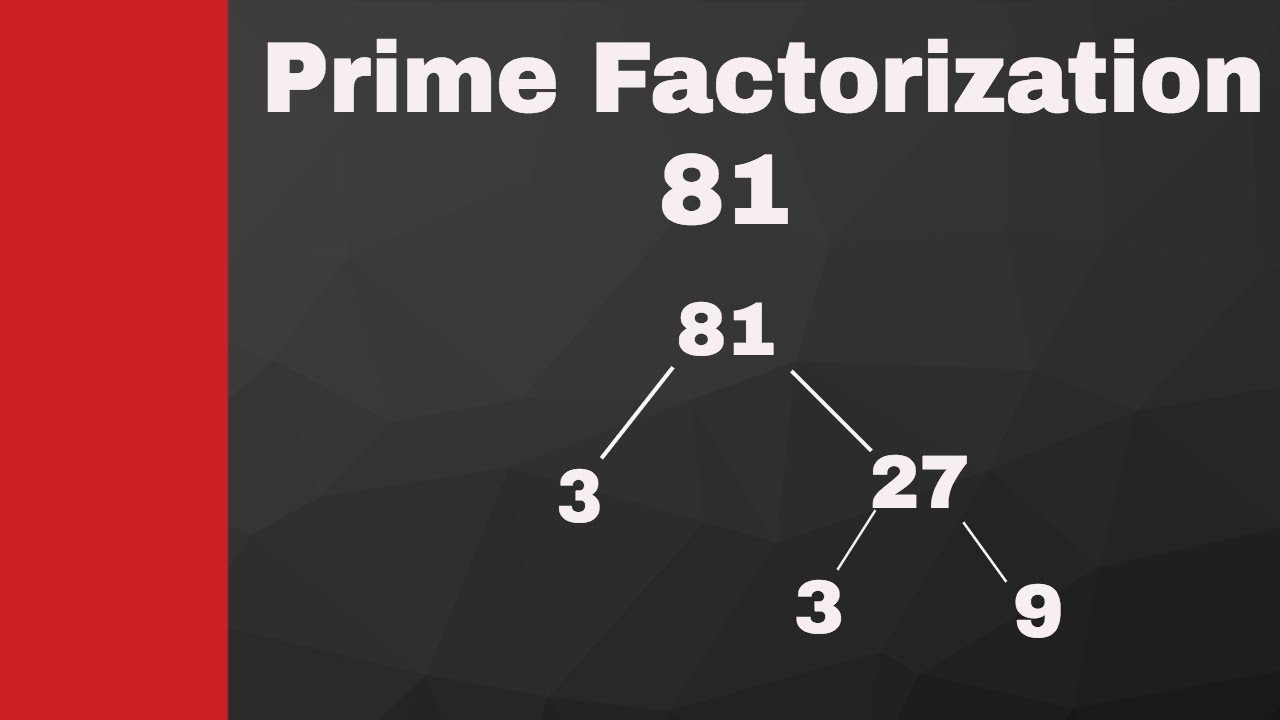
In the maths worksheet for kids to learn prime factorization, it must be developed in a way that kids are able to solve the first few problems in the worksheet easily and, if possible, should be simple enough that kids can solve the problem verbally. Followed by exercises on the factorization of slightly large numbers and including numbers, the factors of which are interesting; for example, number 105, when factorized, gives 3 * 5 * 7, which are the first three prime numbers.
We have heard many times and commonly known that there are infinite numbers, but there are also infinite numbers between any two numbers is something often ignored when looking at the enormity of the variety of numbers. In this article, let’s discuss the concept of prime factorization of numbers.
Most commonly known numbers are the whole numbers which start with 1 and are integers; then we have real numbers, fractions, negative numbers, and complex numbers. For knowing more about numbers, visit the Cuemath website and download the math worksheets related to numbers. Among all these numbers, there is a particular subset of numbers that has caught the fancy of many mathematicians for a couple of centuries.
Among the family of whole numbers are two categories, prime numbers, and composite numbers. Composite numbers are numbers that are divisible by more than two numbers, while prime numbers are those which are divisible by only two numbers, and these two numbers are number ‘1’ and the number itself. As in the case of composite numbers like 15, we can express this number as multiplication of 5 and 3, so numbers 5 and 3 can also be called the factors of 15. By multiplying the factors of the number, we get that number. But in the case of a prime number such as 23, it cannot be shown as multiplication of any two numbers except 23 itself and the number ‘1’.
While composite numbers are more and very often used, it is the set of prime numbers which happens to engage mathematicians across the world since the mystery of how to find the next prime number is still unsolved, and it is also worth mentioning the application of prime numbers in cryptography is widespread. So, as we saw, composite numbers can be divided into factors which are prime themselves but when multiplied, provide the composite number, which leads one to ponder that all composite numbers are in fact made of prime numbers, and thus one can call prime numbers as the building block of composite numbers.
In the maths worksheet prepared for kids to learn prime factorization, it must be developed in a way that kids are able to solve the first few problems in the worksheet easily and, if possible, should be simple enough that kids can solve the problem verbally. Followed by exercises on the factorization of slightly large numbers and including numbers, the factors of which are interesting; for example, number 105, when factorized, gives 3 * 5 * 7, which are the first three prime numbers.
In the worksheets, kids should be able to solve the later part of the problems using the prime factorization method, and the good thing about prime factorization is that kids can themselves check the answer by multiplying the factors together and see if they arrive at the original number which was factorized.
While the concept of factorization is simple, as is often the case with any stream of mathematics, it takes practice to get a grip on the concept, and the technique to calculate and thus solving varying degrees of problem using the worksheet gives the kids required practice and the step by step guide will help them confirm their own answers. In the worksheet, the availability of different types of problems in one place and in a specific order helps kids to journey through the various noteworthy points about the topic and at the end of it makes the kid confident of the skill acquired.
Thus, worksheets for prime factorization should be prepared, keeping in mind that the focus is to be given on finding the solution as well as on the relevance of the whole exercise as well. Kids should be able to appreciate how prime factorization is a useful technique and how many different applications rely on correct prime factorization for its working.
Read more:
- Rick and Morty Season 4 Torrent
- Rick and Morty Torrent
- rick and morty season 3 torrent